
연역법과 귀납법 쉽고 간단하게 이해하기

도서관 목록의 전거 개념과 흐름도
이번에는 사회학, 심리학, 통계학 등의 분야에서 통계분석 용도로 많이 이용되는 척도의 개념과 종류에 대하여 알아보고자 한다. 처음 접하는 사람에게는 다소 낯설게 느껴질 수 있는 개념이므로 쉽게 이해할 수 있도록 별도의 이미지를 제작했다.
먼저 개념을 간단히 집어보자면 척도란 사물이나 사람 등 대상의 특성을 통계상의 수로 표현하기 위해 체계적으로 그 속성에 숫자를 부여한 것을 말한다.
척도의 종류에는 명목척도, 서열척도, 등간척도, 비율척도가 있는데, 각각의 특성과 담고 있는 정보가 다르다.

척도의 4유형 – 명목척도, 서열척도, 등간척도, 비율척도
여기서 4가지 유형의 척도가 담고 있는 정보를 나열했을 때 [명목척도 < 서열척도 < 등간척도 < 비율척도] 순서이며 명목척도가 가장 적은 정보를 담고 있다. 그럼 여기서 언급된 명목척도, 서열척도, 등간척도, 비율척도를 차례대로 하나씩 소개해보고자 한다.
1. 명목척도
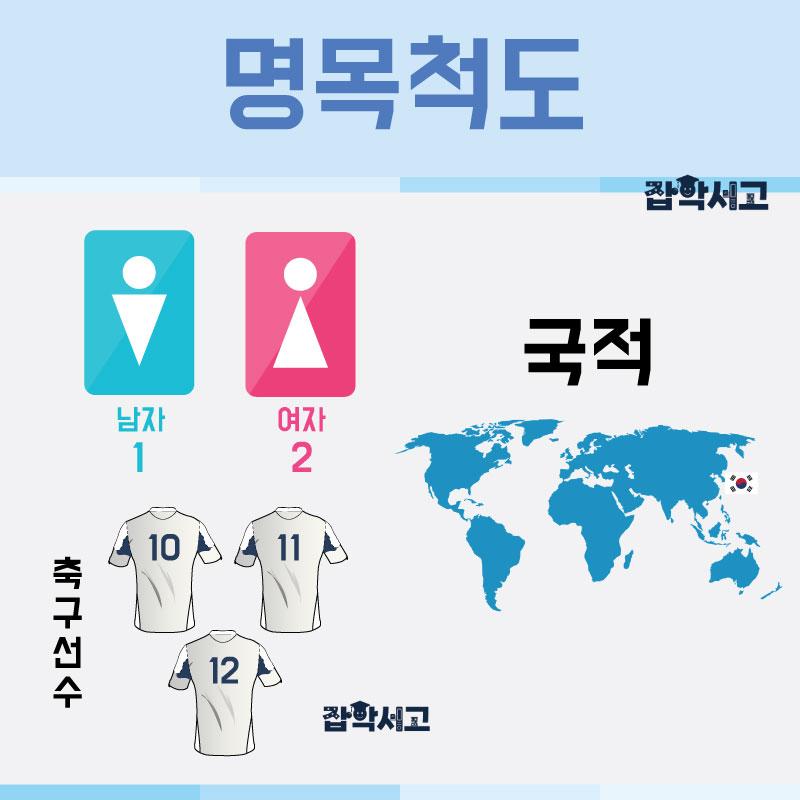
명목척도의 예
먼저 명목척도(명명척도)는 남자(1), 여자(2)처럼 이름이나 명칭이 들어갈 자리에 숫자를 부여한 것으로, 여기서 숫자는 단순히 속성이 다르다는 것을 나타낼 뿐 별다른 정보를 갖지 않는다.
명목척도의 예로는 성별(남자 1, 여자 2), 선수번호(9번, 10번, 11번), 국적(한국, 일본, 중국, 미국) 등 대상을 속성에 따라 구분하기 위한 숫자들이 대표적이다.
비교방법 : 확인, 분류
연산 : =
통계 : 최빈치
적용가능 통계방법 : 비모수통계, 빈도분석, 교차분석
2. 서열척도

서열척도의 예
서열척도는 대상을 구분해주는 명목척도의 특성을 가지면서, 이와 함께 대상의 순위관계에 대한 정보를 담고 있는 척도이다. 다만, 순위 관계를 나타낼 수는 있지만 그 차이가 동일하다고는 볼 수 없다.
대표적으로 시험 성적에 대한 순위 관계(1등, 2등, 3등)와 키 순서(183cm, 177cm, 170cm)와 같은 경우를 예로 들 수 있다.
비교방법 : 순위비교
연산 : =, <, >
통계 : 최빈치, 중앙치
적용가능 통계방법 : 비모수통계, 서열 상관관계
3. 등간척도

등간척도의 예
등간척도는 앞에서 언급한 명목척도와 서열척도에 대한 정보를 가지면서 속성의 차이가 동일하다는 간격(등간) 정보를 포함하는 척도이다. 이 때문에 다른 말로 ‘간격척도’로 불리기도 한다.
등간척도의 가장 대표적은 예로 언급되는 것은 온도와 연도에 관한 정보이다. 오전과 오후 8시에 2시간 동안의 온도 변화를 각각 측정했을 때 10도→20도 / 20도→10도로 측정됐다면 여기서 온도는 동일하게 10도가 변동되었다는 것을 알 수 있다.
또한 연도의 경우도 올림픽과 월드컵의 경우를 고려해봤을 때 2002, 2006 … 2022, 2026 등 동일하게 4년 간격으로 숫자가 변하는 정보를 담고 있다.
비교방법 : 간격비교
연산 : +, -, =, <, >
통계 : 최빈치, 중앙치, 산술평균
적용가능 통계방법 : 모수통계
4. 비율척도

비율척도의 예
비율척도는 앞의 명목, 서열, 등간척도에 대한 정보를 포함하면서 비율에 관한 정보까지 담고 있는 척도이다. 비율척도의 가장 큰 특징은 절대 ‘0’의 값(절대영점)을 가지고 사칙연산(+, -, ×, ÷)이 가능하다는 것이다.
비율척도의 경우를 몸무게로 예로 들면 A가 40kg, B가 65kg, C가 80Kg이라고 했을 때, C는 A보다 몸무게가 2배(×곱셈)가 더 나간다는 정보, C가 B보다 15kg(-뺄셈)이 더 나간다는 정보 등을 알 수 있다.
비교방법 : 절대크기 비교
연산 : +, -, ×, ÷, <, >
통계 : 최빈치, 중앙치, 기하평균, 조화평균 등
적용가능 통계방법 : 모수통계

여기에 통계학에서는 명목, 서열, 등간 정보를 포함해 절대영점과 절대단위를 갖고 특정 항목이나 속성의 수량을 나타내는 절대척도라는 것도 있다. 그러나 보편적으로는 명목, 서열, 등간, 비율척도가 주로 사용되기 때문에 주요 4척도 위주로만 알고 있어도 충분하다.
이상으로 사회과학 분야에서 주로 사용되는 척도인 명목척도, 서열척도, 등간척도, 비율척도의 4가지 유형에 대하여 알아보았다. 본 자료를 통해 위의 4가지 척도 유형을 이해하고 어렵게 느껴질 수 있는 통계에 한걸음 더 다가가는 계기가 되었기를 바란다.






